Minimum Variance Filterbank algorithm is designed to isolate and track one spectrally-compact signal component even though the signal s(t) consists of other unknown interfering signals. It is composed of a group of wideband filters. One such group consisting of L wideband filters is shown inside a dashed rectangular box in Fig (2). The L filters are then linearly combined with weights h(0), ... , h(L-1) to form a resultant filter. So the output of the resultant filter is obtained by linearly combining the respective filtered outputs with their respective weights. The weights h(n) are determined such that the frequency response of the resultant filter is constrained to be unity at a given frequency "w" (called the steering frequency) while the variance/power P in x(t) is minimized. This results in a simple minimization problem similar to the minimum variance distortionless receiver (MVDR) well known in adaptive beamforming. The modulations in the bandpass signal x(t) are analyzed and its average instantaneous frequency (AIF)  is estimated which then serves as the steering frequency during the next processing interval. Since speech formants slowly drift with time, the steering frequency helps move the resultant filter along the formant trajectory thereby tracking the formant frequencies.

AIF tracks and Null tracks of speech utterance “Three”
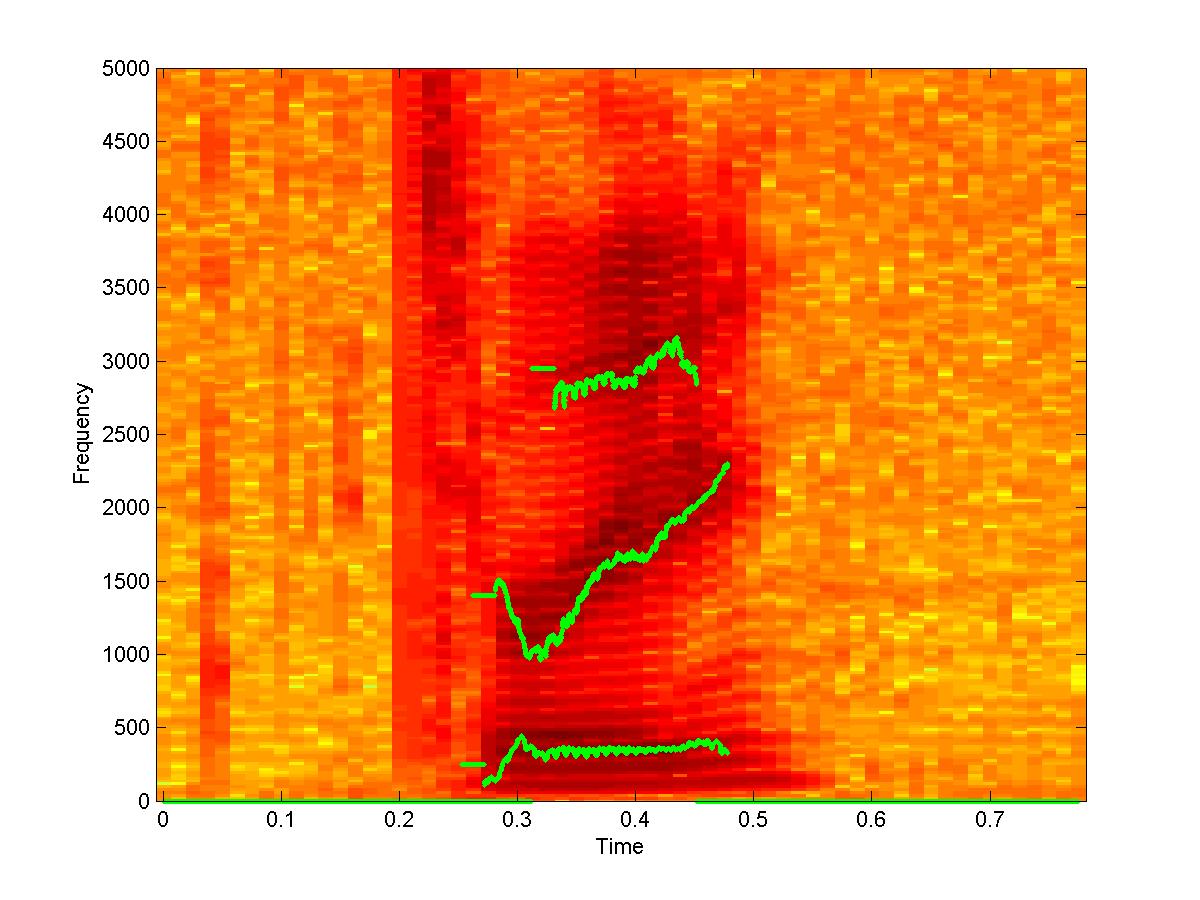Fig 3(a)	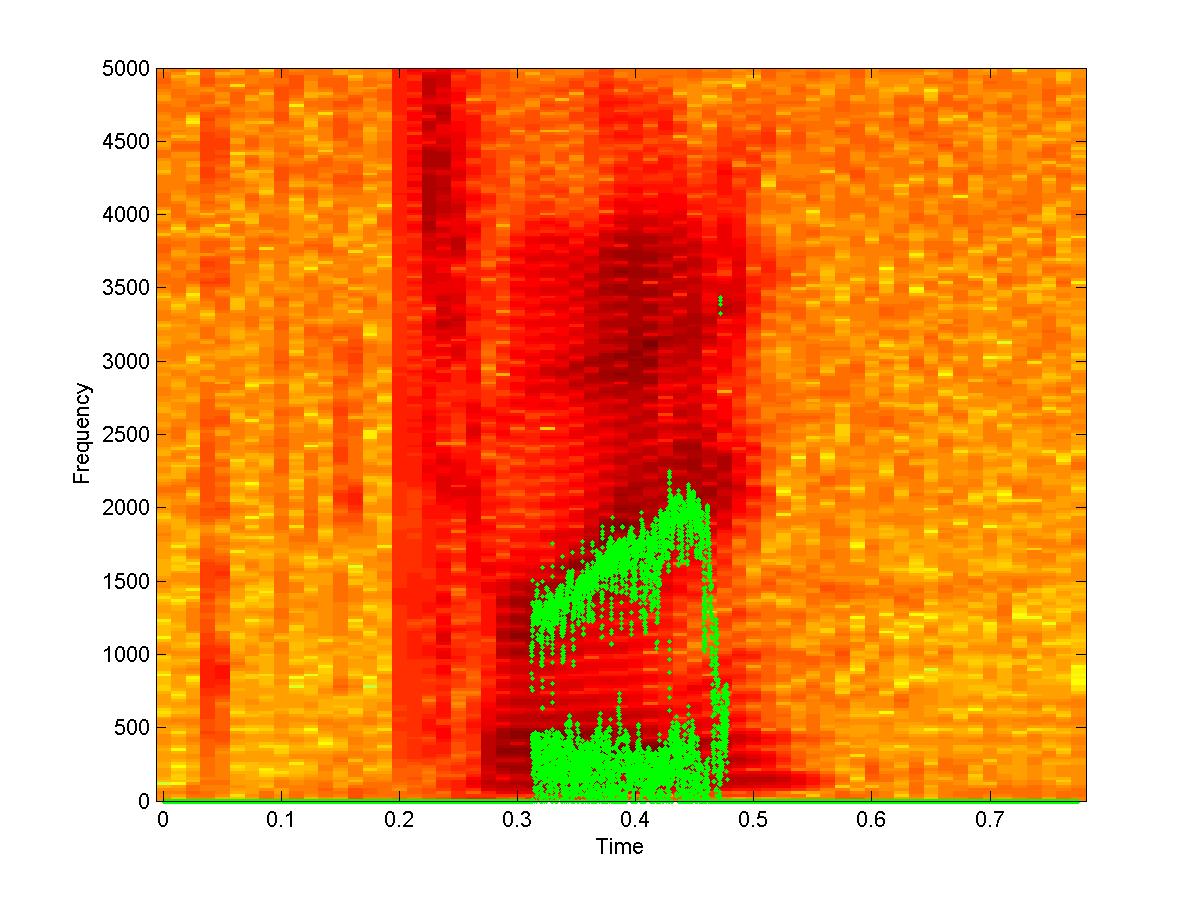Fig 3(b)

The spectrogram of the speech utterance ``Three'' and the formant tracks (AIFs) for three groups of filters obtained by the above procedure are shown in Fig (3a).  Particularly noteworthy is the Fig (3b) which shows the tracks of the nulls of the time-varying resultant filter whose passband stays centered on the third formant (located around 3 kHz). Note that the nulls of this filter are always centered over the first and the second formants, even though these formants themselves are slowly drifting.

Given below are the few examples which shows the formant tracks obtained by the above described algorithm. Clear spectrograms and spectrograms with formant tracks are shown for each example.
 

1. Spectrogram and AIF tracks for speech utterance “Two”
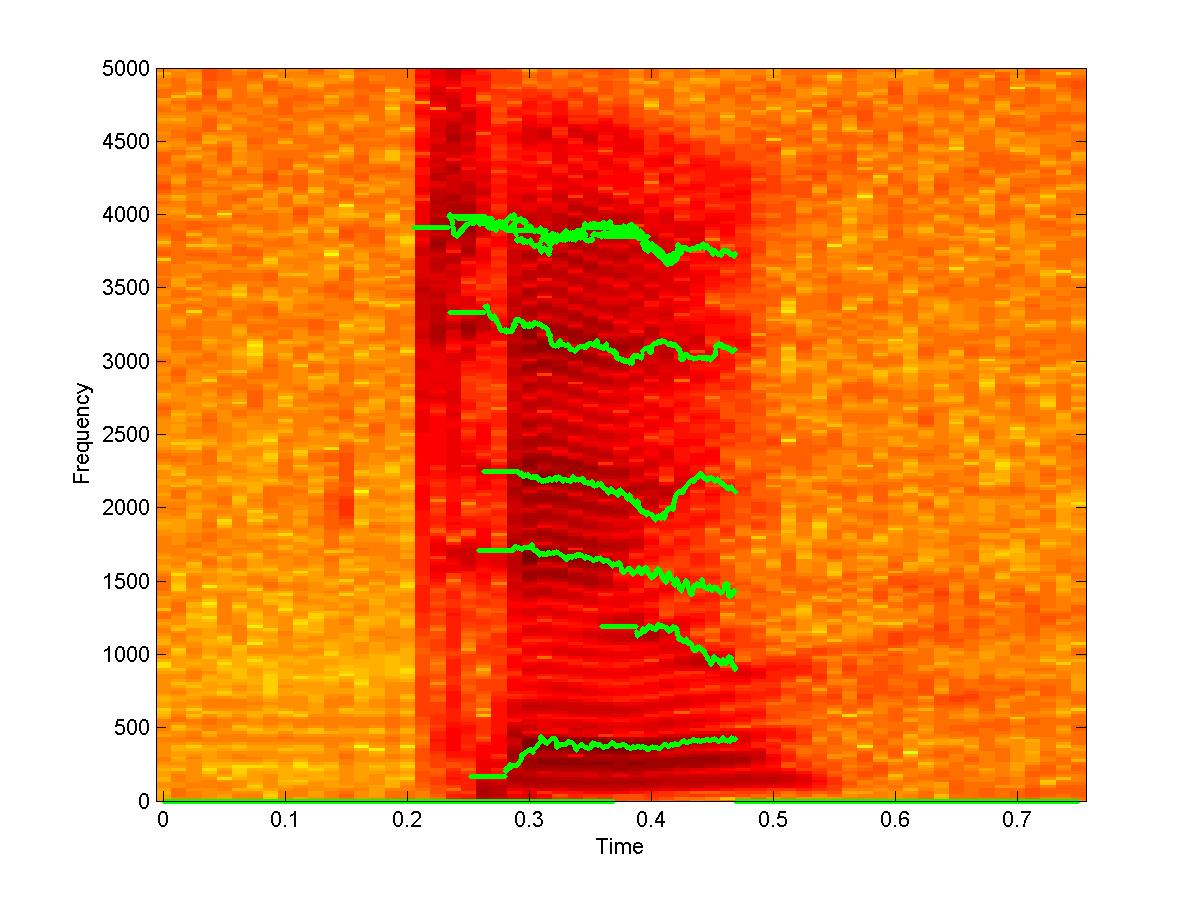2. Spectrogram and AIF tracks for speech utterance “Two Zero Eight Eight”
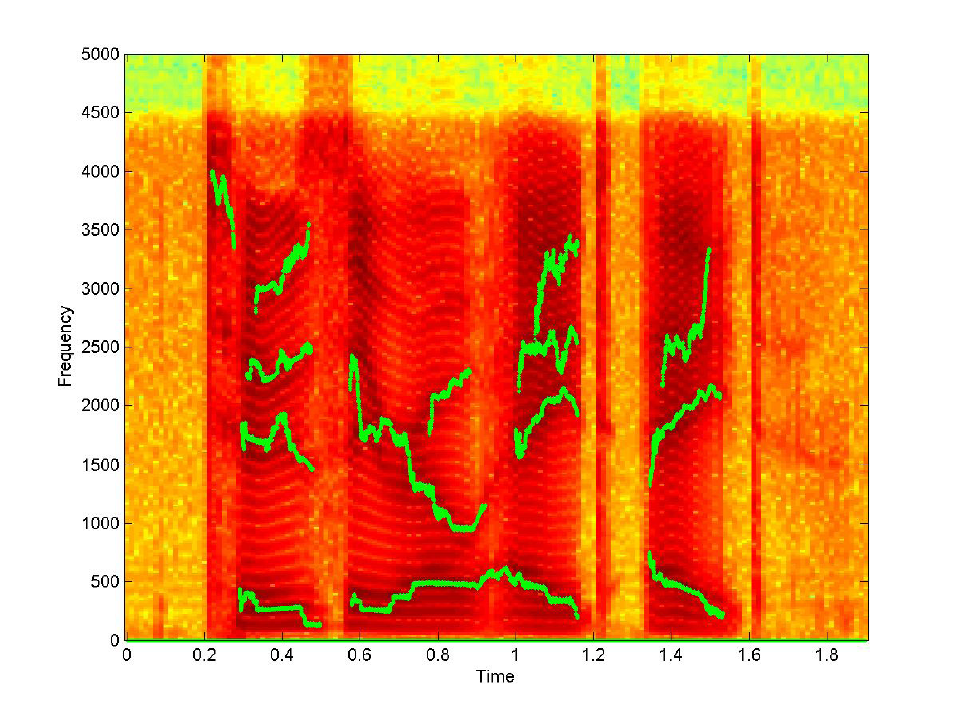3. Spectrogram and AIF tracks for speech utterance “Nine”
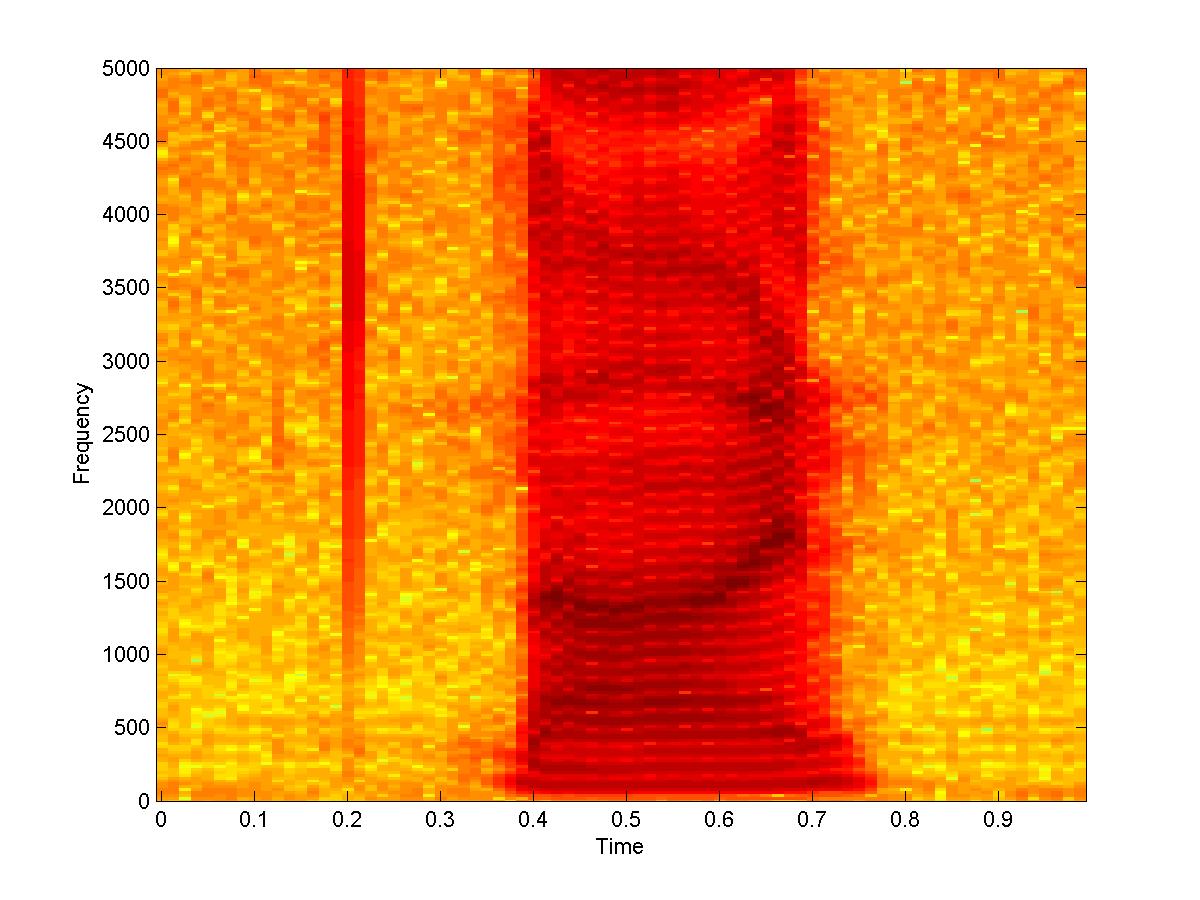4. Spectrogram and AIF tracks for speech utterance “Two Oh Five”
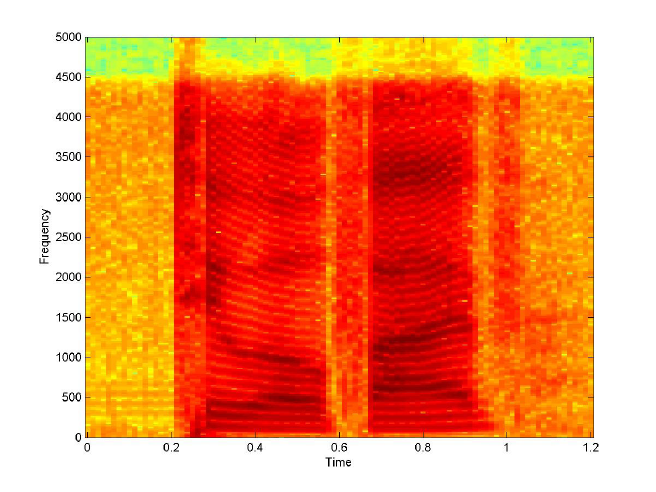5. Spectrogram and AIF tracks for speech utterance “Three Two Zero Zero Zero”
6.  Spectrogram and AIF tracks for speech utterance “Three Oh Three Three Nini Five One”
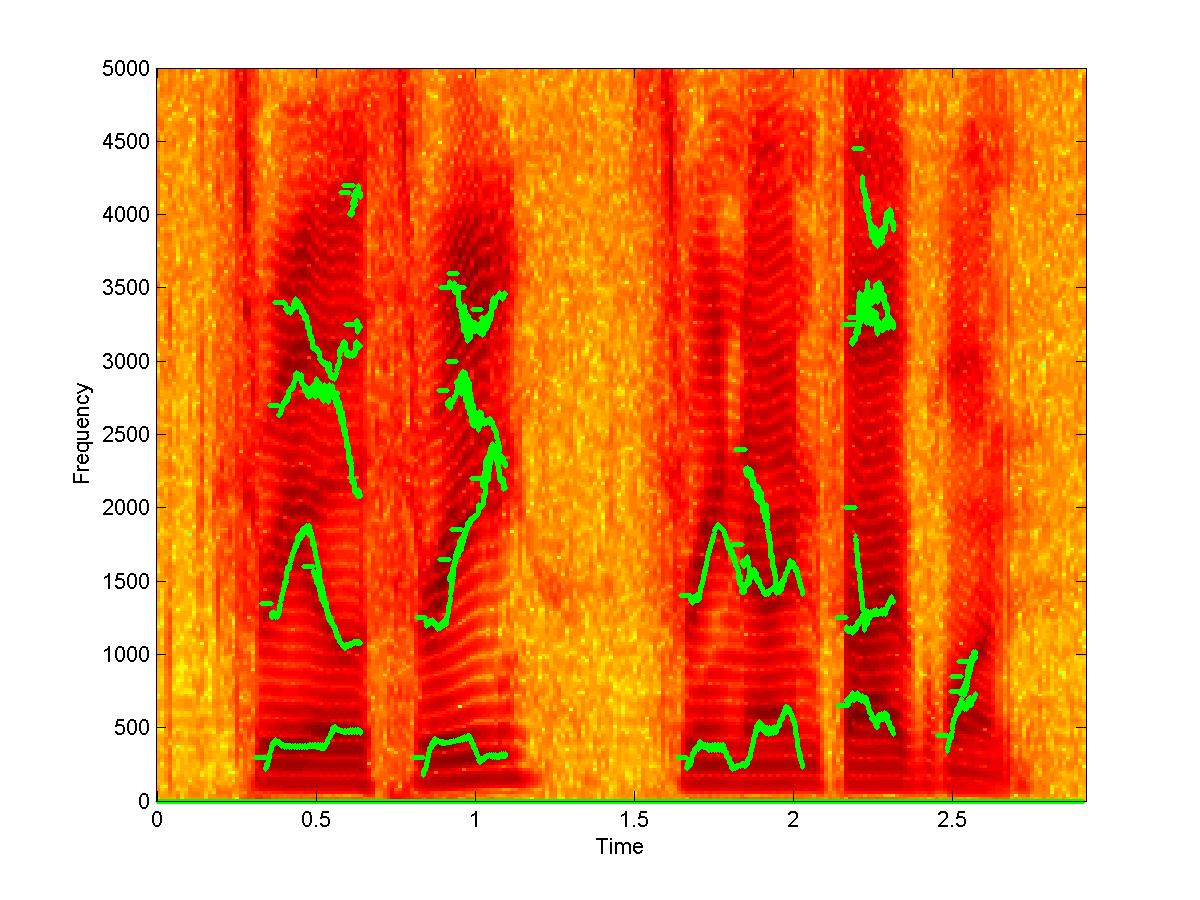7. Spectrogram and AIF tracks for speech utterance “Six Oh Eight Three Eight”

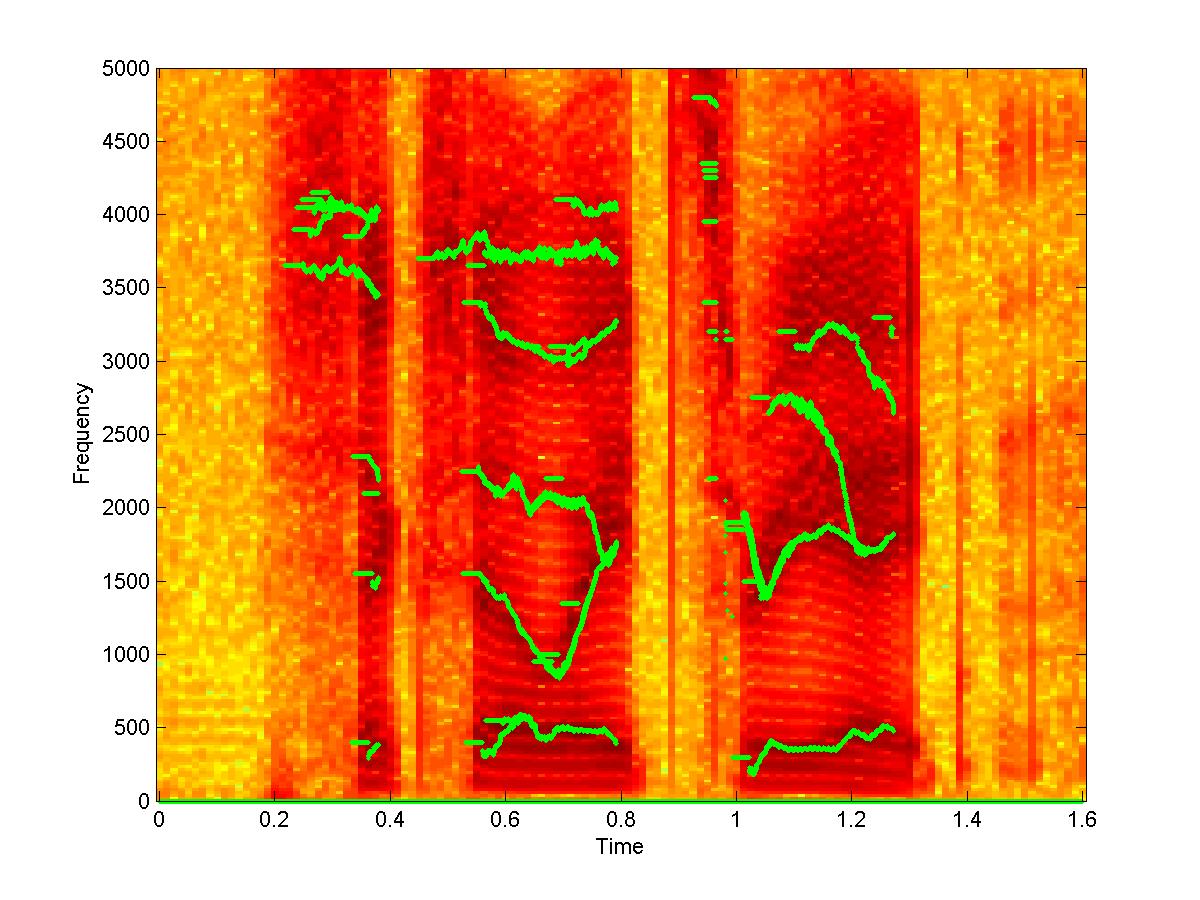Minimum Variance Filterbank algorithm for Spectrally-diffuse  components

Fig 4: MVFB algorithm for spectrally-diffuse signals

Minimum Variance Filterbank algorithm (Fig 4)  for spectrally-diffuse signals is designed to characterize any sudden changes/onsets in the signal. It consists of a bank of narrowband filters which are "Delta w" apart in their center frequencies. The outputs of the filter are compressed by the nonlinearity.  More details on this particular part of work will be provided later.