Opamp exam problem 1


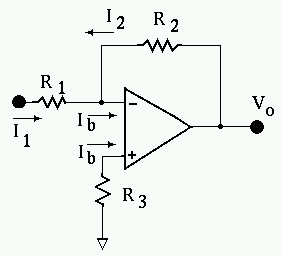
Figure 1
  1. What is the effect of a 1 uA input bias current on the output of the circuit shown in Figure 1?

Answer

Ib = 1 uA
R1 = 10K
R2 = 25K
R3 = 0

The component of Vo due to Ib is

Vo = R2*Ib = 1 uA * 25K = 25 mV

True since
V+ = -R3*Ib

I1 + I2 = Ib

(Vin + R3*Ib)/R1 + (Vo + R3Ib)/R2 = Ib

Multiply by R2

V0 + R3Ib +(R2/R1)[Vin + R3Ib] = R2Ib

Solve for Vo

Vo = -(R2/R1)Vin + Ib[R2 - R3 -R2R3/R1]

The effect of Ib on Vo will be zero if R2 = R3[1 + R2/R1] = R3[(R1+R2)/R1]

R3 = R1R2/(R1+R2)

This is the well known method for reducing the effect of Ib. That is, set the impedances seen by the non-inverting input equal to the impedance seen by the inverting input.

But if R3 = zero, as in this problem,

Vo = -(R2/R1)Vin + IbR2

Also, with R3 = 0, V- = V+ = 0, and therefore I1 = 0
so I2 = Ib